unk

题目

用割圆术逼近圆周率 $\pi$ 的方法如下：

取单位圆，作其内接正六边形，并重复以下步骤：

1. 连接圆心与正 $n$ 边形每条边终点并延长，交圆于 $n$ 个新的点；将原 $n$ 边形各顶点和这 $n$ 个新的点顺次连接，便形成了正 $2n$ 边形。
2. 若原正 $n$ 边形边长 $A_n$（注意到 $A_6=1$）：将正 $n$ 边形分成 $n$ 个等腰三角形，可求出三角形底边上的高 $H_n$。
3. 利用 $A_n$ 和 $H_n$ 可求出正 $2n$ 边形比正 $n$ 边形多出来的面积，进而求出正 $2n$ 边形的面积，它是 $\pi$ 的近似值。
4. 利用 $1-H_n$ 和 $A_n$，可求出 $A_{2n}$，以供下次循环使用。

设计程序，打印出单位圆内接正 $6\cdot 2^n(n=0,1,2,...)$ 边形的面积。不出意外的话，它应该越来越接近 $\pi$。

解析

1. 正六边形面积：$\frac{\sqrt{3}}{4}{a}^2\cdot 6$。
2. todo

解答

#include <stdio.h>
#include <math.h>

int main() {
    double length = 1.0;
    int n = 6;
    double area = n * length * length * 0.25 * sqrt(3);

    for (int i = 0; i < 25; i++) {
        double height = sqrt(1 - length * length / 4.0);
        double added_area = n * (1 - height) * length / 2.0;
        area += added_area;
        length = sqrt((1 - height) * (1 - height) + length * length / 4.0);
        n *= 2;
        printf("正 %d 边形面积：%.14lf\n", n, area);
    }

  return 0;
}

可能的输出：

正 12 边形面积：3.00000000000000
正 24 边形面积：3.10582854123025
正 48 边形面积：3.13262861328124
正 96 边形面积：3.13935020304687
正 192 边形面积：3.14103195089051
正 384 边形面积：3.14145247228546
正 768 边形面积：3.14155760791186
正 1536 边形面积：3.14158389214832
正 3072 边形面积：3.14159046322805
正 6144 边形面积：3.14159210599927
正 12288 边形面积：3.14159251669216
正 24576 边形面积：3.14159261936538
正 49152 边形面积：3.14159264503369
正 98304 边形面积：3.14159265145077
正 196608 边形面积：3.14159265305504
正 393216 边形面积：3.14159265345610
正 786432 边形面积：3.14159265355637
正 1572864 边形面积：3.14159265358144
正 3145728 边形面积：3.14159265358770
正 6291456 边形面积：3.14159265358927
正 12582912 边形面积：3.14159265358966
正 25165824 边形面积：3.14159265358976
正 50331648 边形面积：3.14159265358979
正 100663296 边形面积：3.14159265358979
正 201326592 边形面积：3.14159265358979

补充

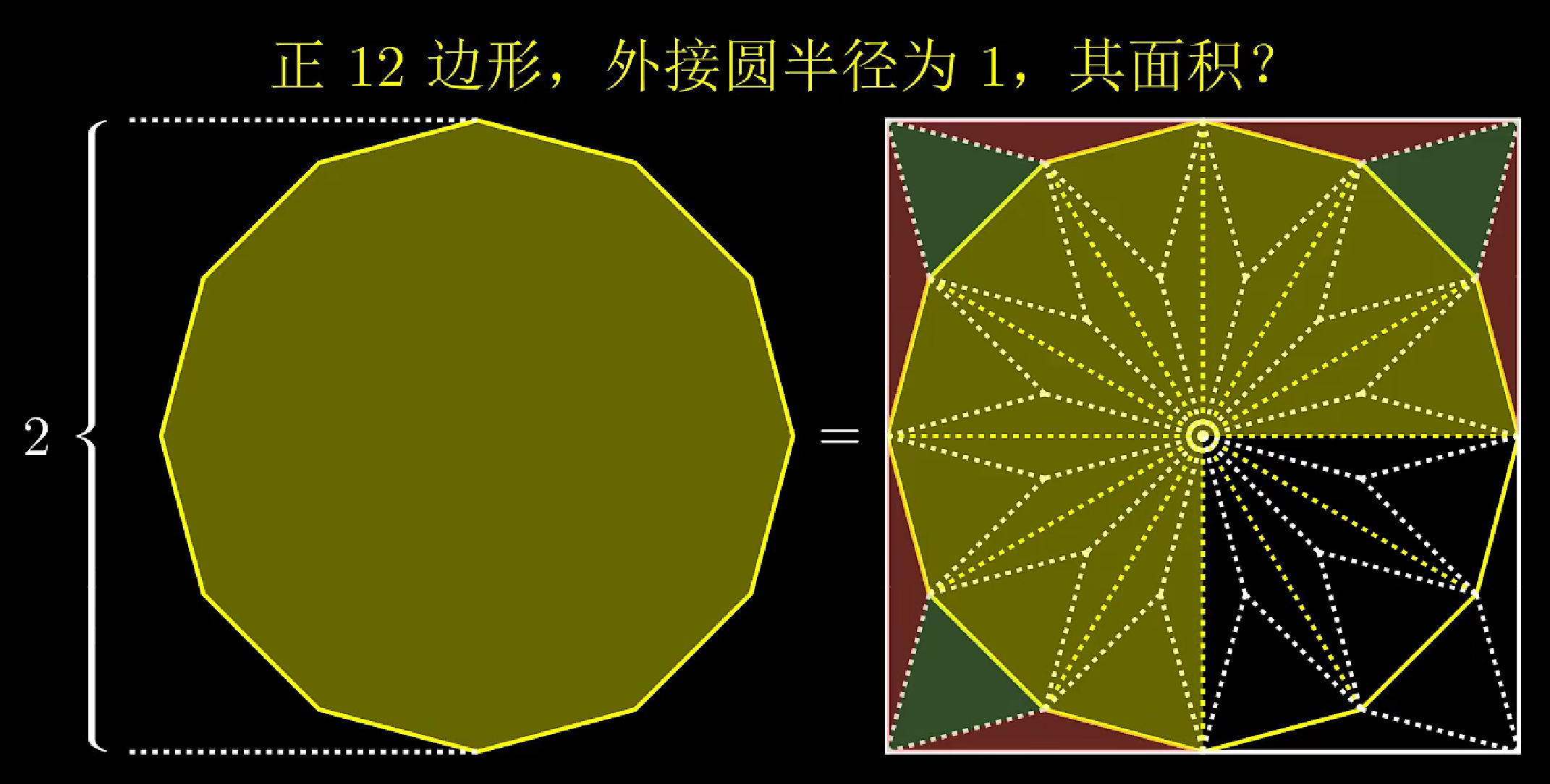
可以看到，正 12 边形的面积正好是 3。下面这个图可以很好地解释：